Discretização Espacial

A preferência pelo uso do método dos volumes finitos reside na capacidade do método garantir a conservação do sistema, visto que as fronteiras para cada volume de controle são definidas e únicas. O volume de controle discretizado tem suas propriedades de interesse analisadas em seu ponto central, e o balanço é feito de acordo com os fluxos nas fronteiras de cada volume.

Método dos Volumes Finitos

De acordo com as hipósteses adotadas, o problema da sedimentação pode ser simplificado para um domínio unidimensional. Dessa forma, a discretização espacial tem apenas uma componente, \(z\).

A figura abaixo ilustra a discretização do domínio unidimensional, em volumes finitos:

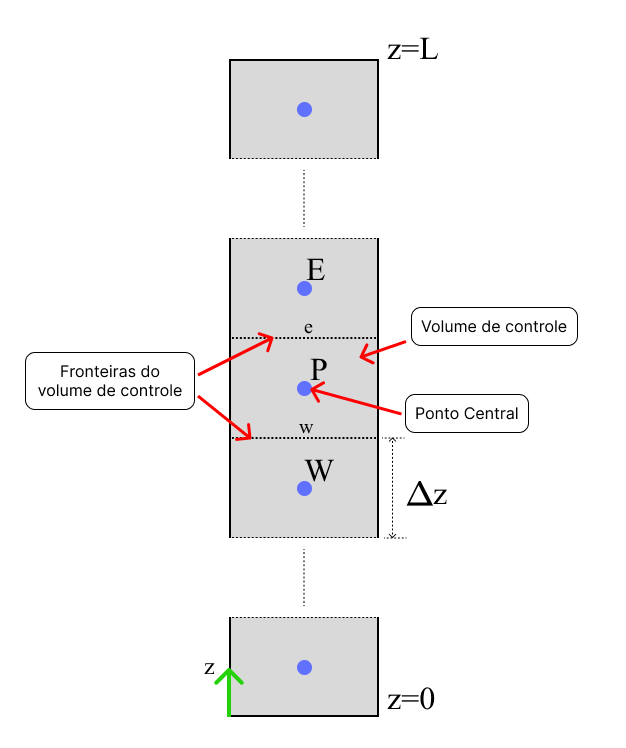
Cada volume, ou célula, compartilha uma fronteira única com as células vizinhas. De tal modo, que a variação da concentração de uma fase, seja resultado do fluxo da mesma indo para os volumes vizinhos.

Importante notar que no fim da coluna, \(z=0\), e no topo da coluna, \(z=L\), existe apenas uma fronteira, visto que estão nos limites do domínio.

Important

Embora a única região que tenha um comportamento compressivo seja a região da formação do sedimento, foi decidido simular o domínio como um todo, de modo que a separação entre regiões seja resultado da simulação da sedimentação. Outra opção seria rastrear as interfaces a partir da solução analítica, utilizando condições de salto de interface.

A equação da conservação de massa é então discretizada, de tal forma:

\[\frac{{\partial {\varphi _{P}}}}{{\partial t}} + \frac{{{{\left( {{\varphi _E}{v_e}} \right)}} - {{\left( {{\varphi _P}{v_w}} \right)}}}}{{\Delta z}} = 0\]

Aplicando as condições de contorno, no fundo e no topo da coluna, para \(z=0\) (fundo):

\[\frac{{\partial {\varphi _{P}}}}{{\partial t}} + \frac{{{{\left( {{\varphi _E}{v_e}} \right)}}}}{{\Delta z}} = 0\]

E para \(z=L\) (topo):

\[\frac{{\partial {\varphi _{P}}}}{{\partial t}} - \frac{{{{\left( {{\varphi _P}{v_w}} \right)}}}}{{\Delta z}} = 0\]

Como não existe um volume definido nas interfaces entre os nós, não é possível definir uma concentração local. Assim, o valor da concentração é aproximado pela concentração do nó imediatamente acima.

Essa estratégia visa garantir a redução do fluxo de sólidos em um volume quando sua concentração atinge o valor da concentração máxima (Rocha et al.1).

Variação de Seção Transversal

O efeito de variação da seção transversal da região anular pode ser modelado a partir do balanço de massa entre as células adjacentes a descontinuidade geométrica. O fluxo de sólidos do nó anterior a descontinuidade (1) é imediatamente injetado no volume posterior (2), assim como ilustra a figura a seguir:

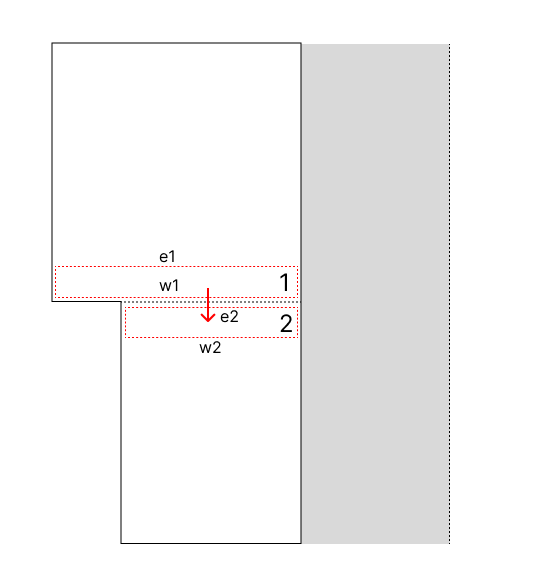
A área efetiva de vazão de sólidos é igual a menor área transversal entre o volume anterior e posterior à fronteira:

\[ \begin{align}\begin{aligned}A_e = min(A_{P-1}, A_P)\\A_w = min(A_P, A_{P+1})\end{aligned}\end{align} \]

Aplicando o balanço de massa no volume de controle 2:

\[\frac{{\partial {\varphi _{P}}}}{{\partial t}} + \frac{{{{\left( {{\varphi _E}{v_e} A_e} \right)}} - {{\left( {{\varphi _P}{v_w} A_w} \right)}}}}{{\Delta z A_P}} = 0\]

Malha não uniforme

O domínio considerando a variação de seção transversal é construído a partir da informação da máxima altura, e seu respectivo raio. A figura abaixo ilustra essa relação:

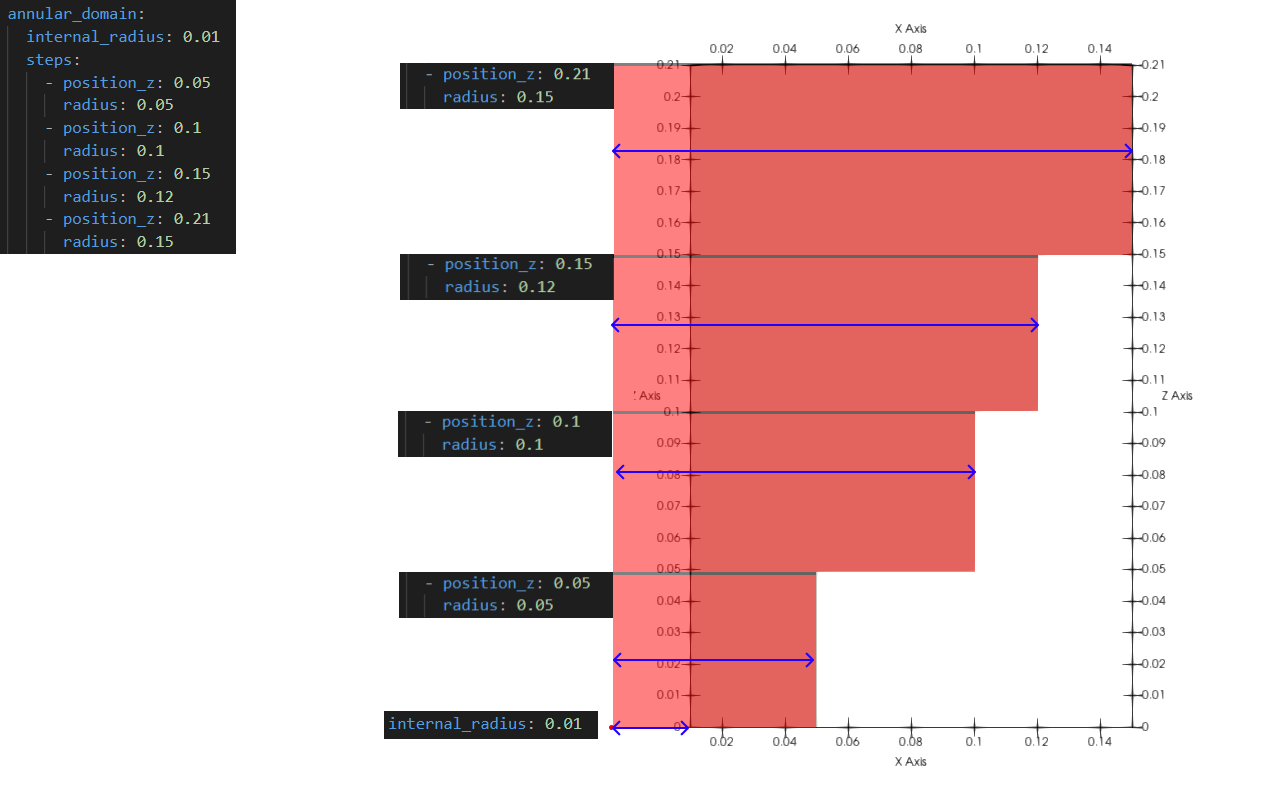
Possivelmente, a posição informada entre seções com raios distintos pode não coincidir com a fronteira das células de uma malha uniforme. Nesse caso, é necessário utilizar uma malha não uniforme para garantir que a geometria constuída conforme com as posições das variações informadas.

Note

Consultar a seção Software - Variação de seção transversal para mais detalhes de como habilitar a variação de seção transversal no software.