Discretização Temporal

Para a solução do sistema de equações discretizadas, obtidas a partir da equação da conservação de massa, o método Runge-Kutta de 4ª ordem foi utilizado para realizar o avanço temporal.

De forma genérica, a aplicação do método RK4 permite usar passos de tempos maiores, visto que o avanço temporal é feito com base em inclinações intermediárias entre os passos de tempo.

A sedimentação trata-se de um problema de valor inicial, visto que no primeiro instante de tempo, a solução se encontra homogeinizada, de forma que:

\[\varphi _{s} (z, t=0) = \varphi _{0}\]

Dessa forma, o termo de acúmulo de sólidos é aproximado pela média ponderadas das inclinações intermediárias:

\[\frac{{\partial {\varphi _{sP}}}}{{\partial t}} = \frac{\varphi _{P} ^ {t + 1} - \varphi _{P} ^ {t}}{{\Delta t}} = \frac{(k_1 + 2k_2 + 2k_3 + k_4)} {6}\]

E as inclinações \(k\), aplicando o método de Runge-Kutta de 4ª ordem:

\[\begin{split}{k_1} &= - \frac{{{\varphi _E}{v_e} - {\varphi _P}{v_w}}}{{\Delta z}} \hfill \\ {k_2} &= - \frac{{\left( {{\varphi _E} + \frac{\Delta t}{2}{k_1}} \right){v_e} - \left( {{\varphi _P} + \frac{\Delta t}{2}{k_1}} \right){v_w}}}{{\Delta z}} \hfill \\ {k_3} &= - \frac{{\left( {{\varphi _E} + \frac{\Delta t}{2}{k_2}} \right){v_e} - \left( {{\varphi _P} + \frac{\Delta t}{2}{k_2}} \right){v_w}}}{{\Delta z}} \hfill \\ {k_4} &= - \frac{{\left( {{\varphi _E} + \Delta t {k_3}} \right){v_e} - \left( {{\varphi _P} + \Delta t {k_3}} \right){v_w}}}{{\Delta z}} \hfill \\\end{split}\]

Note

Se faz necessário atualizar o valor das velocidades das fronteiras \(v_e\) e \(v_w\), entre os cálculos de cada inclinação \(k_i\), de forma que seja refletida a correção do valor da concentração \(\varphi _P + \frac{\Delta t}{2} k_i\) no cálculo das velocidades.

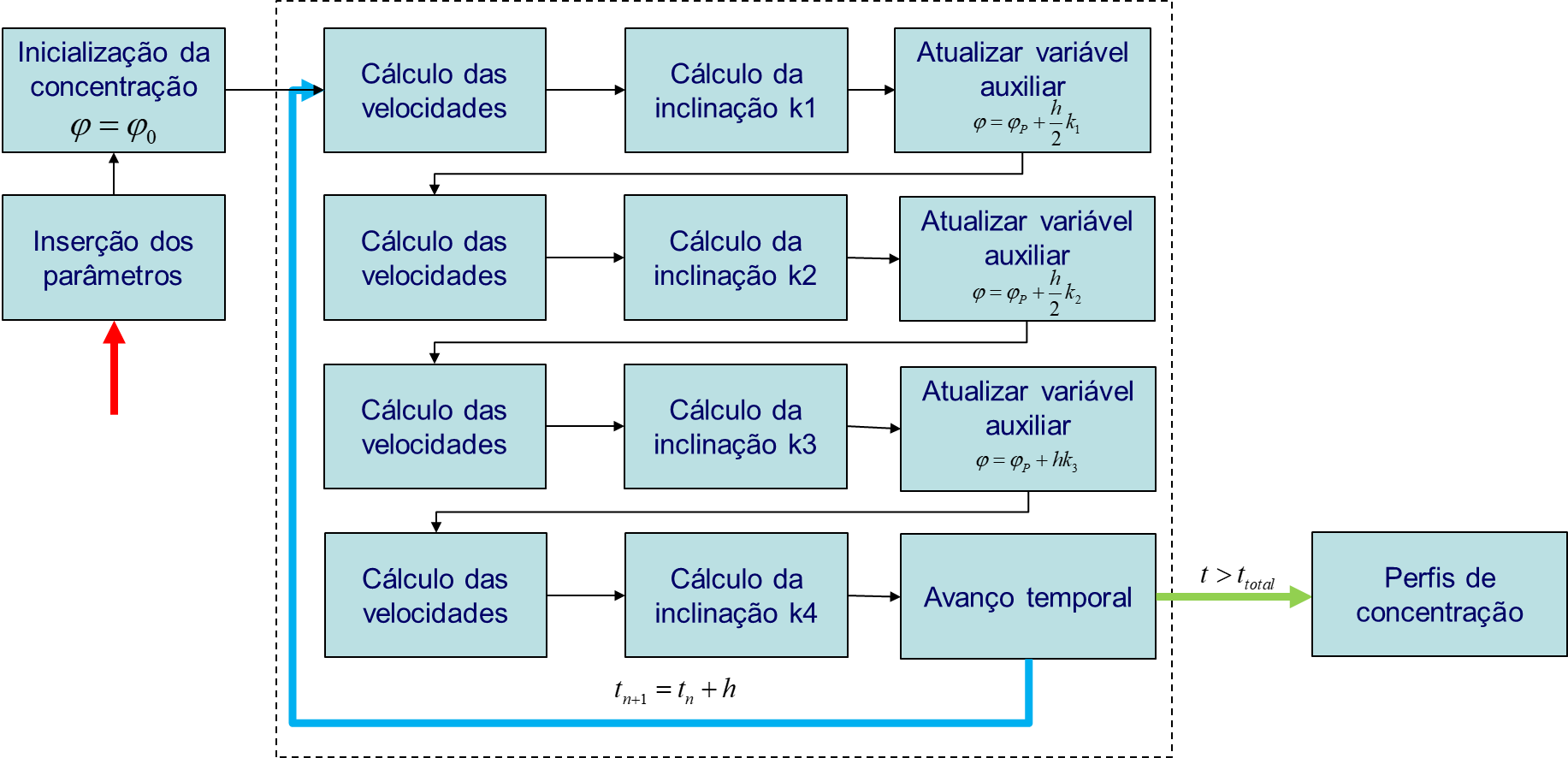
A sequência de cálculos pode ser consultada na abaixo, que implementa as equações previamente apresentadas, para a solução temporal da sedimentação: